EPJ B Highlight - Ultracold gases in time-dependent magnetic fields
- Details
- Published on 04 February 2020
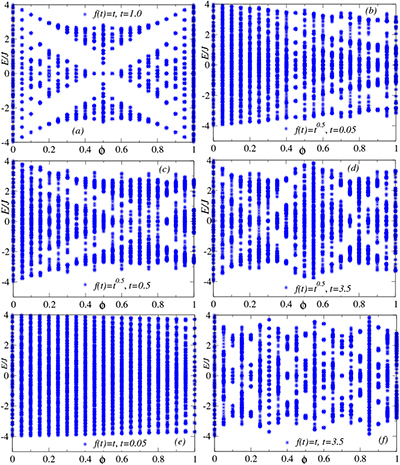
The phase transitions of an ultracold gas under a fluctuating magnetic field show interesting patterns, particularly a loss of symmetry in the energy spectrum that is well observed in the disappearance of the ‘Hofstadter’s butterfly’ effect.
It is now technically possible to hold groups of atoms at temperatures that are only a few hundredths of a degree above absolute zero. This so-called ‘ultracold gas’ loaded in an optical lattice is an extremely powerful platform to study quantum mechanical phenomena including phase transitions, due to the excellent control of experimental parameters, such as potential depths, inter-particle interaction strengths and lattice parameters. Sk Noor Nabi from Zhejiang University in Hangzhou, China and colleagues in the Indian Institute of Technology, Guwahati, India, have studied the phase transition between the Mott insulating (MI) and superfluid (SF) states of such a gas in a time-dependent synthetic magnetic field. Their results, published in EPJ B, show that the energy spectrum of the gas loses symmetry in the fluctuating magnetic field. This is observed in the disappearance of the striking ‘Hofstadter’s butterfly’ effect seen in the energy spectrum under a constant magnetic field.
The physics of an ultracold gas – put another way, of interacting, neutral bosons at close to absolute zero – can be described mathematically with the Bose-Hubbard model. Using this theory, Nabi and his co-workers modelled a neutral ultracold gas in a synthetic magnetic field with a magnetic flux that varied over time. Plotting the phase diagrams at different time points and for different values of magnetic flux showed some quite dramatic changes in the shape of the boundary between the MI (insulating) and SF (zero viscosity) states. Thus, the stability of the MI phase and hence the critical location of the phase transition depends upon the particular choice of time dependent gauge field. They also showed that the symmetry of the energy spectrum under a constant magnetic field was lost once time dependence was introduced, leading to the disappearance of the characteristic Hofstadter’s butterfly pattern.
The Bose-Hubbard model is important for the study of quantum entanglement, which has many applications in quantum information theory. Therefore, studies like this one – which may on the surface seem rather obscure – may come to have ‘real world’ applications when quantum computers become practicable.
S.N. Nabi, S. Dutta and S. Basu (2020), Ultracold gases in presence of time-dependent synthetic gauge field, European Physical Journal B 93:3, DOI: 10.1140/epjb/e2019-100495-6




